[最も人気のある！] 乗法 の 公式 181429

それでは公式を見ていきましょう。 1 確率を求める公式 まずは確率を求めるための公式を挙げていきます。 11 基本の公式 確率において基本となる公式は 計算方法;中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード・印刷 根号を含む複雑な式は、なるべく簡単な形に変形してから値を代入し、分配法則や乗法公式を使って√を含む式を計算する練習問題プリントです。 乗法公式を4つ覚えよう！ まずは4つの乗法公式を覚えましょう！ $$(xa)(xb)=x^2(ab)xab$$ $$(ab)^2=a^22abb^2$$ $$(ab)^2=a^22abb^2$$ $$(ab)(ab)=a^2b^2$$ 覚えましょうしょうと言ってもこれが覚えてもなかなか使いにくいですよ

中学数学 式の展開 乗法公式 中学数学の無料オンライン学習サイトchu Su

乗法 の 公式

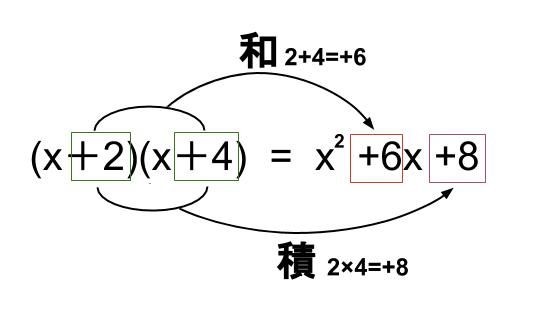
乗法 の 公式- 展開の過程は次の通りですが、上記の公式をそのまま覚えてしまうと楽です。 \((a bi)(c di)\) \(= a \cdot c a \cdot di bi \cdot c bi \cdot di\)だね。 すると、 (x1)(x2) = x^2 (12) x (1×2) = x^2 3x 2

乗法公式 X A X B Youtube

 覚えておくと便利かもしれない乗法公式 ( a b) ( b c) ( c a) = a 2 b a b 2 b 2 c b c 2 c 2 a c a 2 2 a b c (ab) (bc) (ca)\\=a^2bab^2b^2cbc^2c^2aca^22abc (a b)(b c)(c a) = a2b ab2 b2c bc2 c2a ca2 2abc ( a b c) 3 = a 3 b 3 c 3 3 ( a 2 b a b 2 b 2 c b c 2 c 2 a c a 2) 6 a b c乗法 の慣用句・熟語 (2) 出典： デジタル大辞泉（小学館） じょうほうこうしき乗法公式 多項式の積を和の形に直す公式。 多項式を展開するときに使う。 平方の公式：（a＋b）2＝a2＋2ab＋b2、和と差の積の公式：（ab）（a－b）＝a2－b2、たす解説リクエスト 解説リクエストフォーム 問題名 問題番号 mail コメント 展開_ 例題と練習 乗法公式1_ 例題と練習 乗法公式2_ 例題と練習 展開 (おきかえ)_ 例題と練習 いろいろな展開_ 例題と練習 展開 (単項式と多項式の乗除1) 展開 (単項式と多項式の乗除

 展開の4つの基本公式 展開についての，基本的な4つの公式を書きます． これらは，左辺を実際に展開すれば導くことができるので，一度は自分で計算してみてください． さて，4つの公式があるとはいえ， ひとまずは一番上の公式 を使えるようになり 以前、基本展開の公式で二次式の展開について見ました。ここでは、三次式の場合では、式の展開がどうなるかを見ていきます。 三次式の展開 今までに、 $(xy)^2=x^22xyy^2$ などの「2乗の展開」は計算し 2番と3番で後ろについている2は、2乗の意味です。 この4種類も、カッコを外すわけなので、式の展開のように4回かけ算をするやり方でも出来ます。 しかし、乗法「公式」と呼ばれるくらいなので、もっと簡単に解くことが出来ます。 (xa) (xb)=x2 (ab)xab (ab)2=a22abb2 (ab)2=a22abb2 (xy) (xy)=x2y2 このように、この4種類に関してはほぼ暗算で完結してし

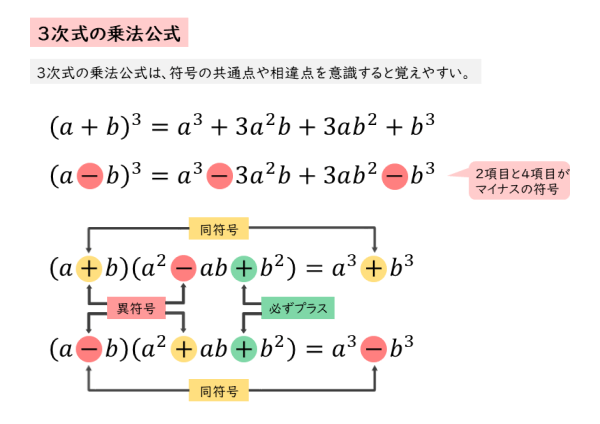
3乗の式の展開には、次の4つの乗法公式を覚えましょう。 ・ (a＋b)³＝a³＋3a²b＋3ab²＋b³ ・ (a－b)³＝a³－3a²b＋3ab²－b³ ・ (a＋b) (a²－ab＋b²)＝a³＋b³ ・ (a－b) (a²＋ab＋b²)＝a³－b³ まずは、本当に公式が成り立つか、それぞれ地道に展開してみましょう。 こちらの乗法公式は、かっこに二乗がついているときに使うことができます。 使い方は簡単！ 2乗 ⇒ 2倍して掛ける ⇒ 2乗 この順に計算すればOKです。 これも例題を使ってやり方を確認しておきましょう。 次の式を展開しなさい。 $$(x3)^2$$ 2乗 ⇒ 2倍して掛ける ⇒ 2乗 この順に計算ピタゴラスの定理 や オイラーの公式 などから以下の基本的な関係が導ける 。 cos 2 ⁡ θ sin 2 ⁡ θ = 1 {\displaystyle \cos ^ {2}\theta \sin ^ {2}\theta =1\!} ここで sin2 θ は (sin (θ))2 を意味する。 この式を変形して、以下の式が導かれる： sin ⁡ θ = ± 1 − cos 2 ⁡ θ {\displaystyle \sin \theta =\pm {\sqrt {1\cos ^ {2}\theta }}}

2

多項式の乗法の公式 数学i フリー教材開発コミュニティ Ftext

 ④ 公式の利用 因数分解は問題によって解き方が異なる場合があります。 いろいろな問題パターンに対応できるように、公式を使って因数分解をするやり方もあります。 先ほどの"乗法公式"をもう一度見てみましょう！乗法公式とは 式を展開するときに、次の公式がよく用いられます。 ①： (a＋b)²＝a²＋2ab＋b² ②： (a－b)²＝a²－2ab＋b² ③： (a＋b) (a－b)＝a²－b² ④： (x＋a) (x＋b)＝x²＋ (a＋b）x＋ab ⑤： (ax＋b) (cx＋d)＝acx²＋ (ad＋bc)x＋bd これらの公式乗法公式とよばれる公式です、 後の 因数分解 という単元でとても大切になるので、必ず覚える ようにしましょう。 覚えるため行列式の基本的な性質と公式 基本的な性質 行や列の入れ替え 同一の列を持つ行列式は $0$ 同一の行を持つ行列式は $0$ 行ベクトルが定数倍された場合 列ベクトルが定数倍された場合 全体が定数倍された場合 行ベクトルが和になっている行列式 列ベクトルが和になっている行列式

乗法公式 応用 X A 2 Youtube

乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係

 これで(xa)(xb)の展開公式もマスターしたね。 この乗法公式なら1瞬でとけちゃう。 たとえば、 (x 1) (x 2)っていう計算式があったとしよう。 公式で計算すれば瞬殺さ。 公式にあてはめてみると、 a = 1; 4つの乗法公式の覚え方を紹介 中学三年生で学ぶ、乗法公式は次の4つがあります。 \begin{align} (xa)(xb) & = x^2(ab)xab \\ (ab)^2 & = a^22abb^2 \\ (ab)^2 & = a^22abb^2 \\ (ab)(ab) & = a^2b^2 \end{align} 学校では、これらの公式を暗記するように言われますが、なかなか覚えにくいものですよね。 「覚えなくとも力技で解けてしまうから覚えなくてもいいや！」多項式と単項式の乗法除法 式の展開 乗法公式 (xa) (xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_ (xa) (xb) 因数分解3_2乗 因数分解4_ (xa) (xa) 因数分解 おきかえ 共通因数をくくりだした後さらに因数分解 項を分けて因数分解する1 (発展) 項を分けて因数分解する2 (発展)

乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係

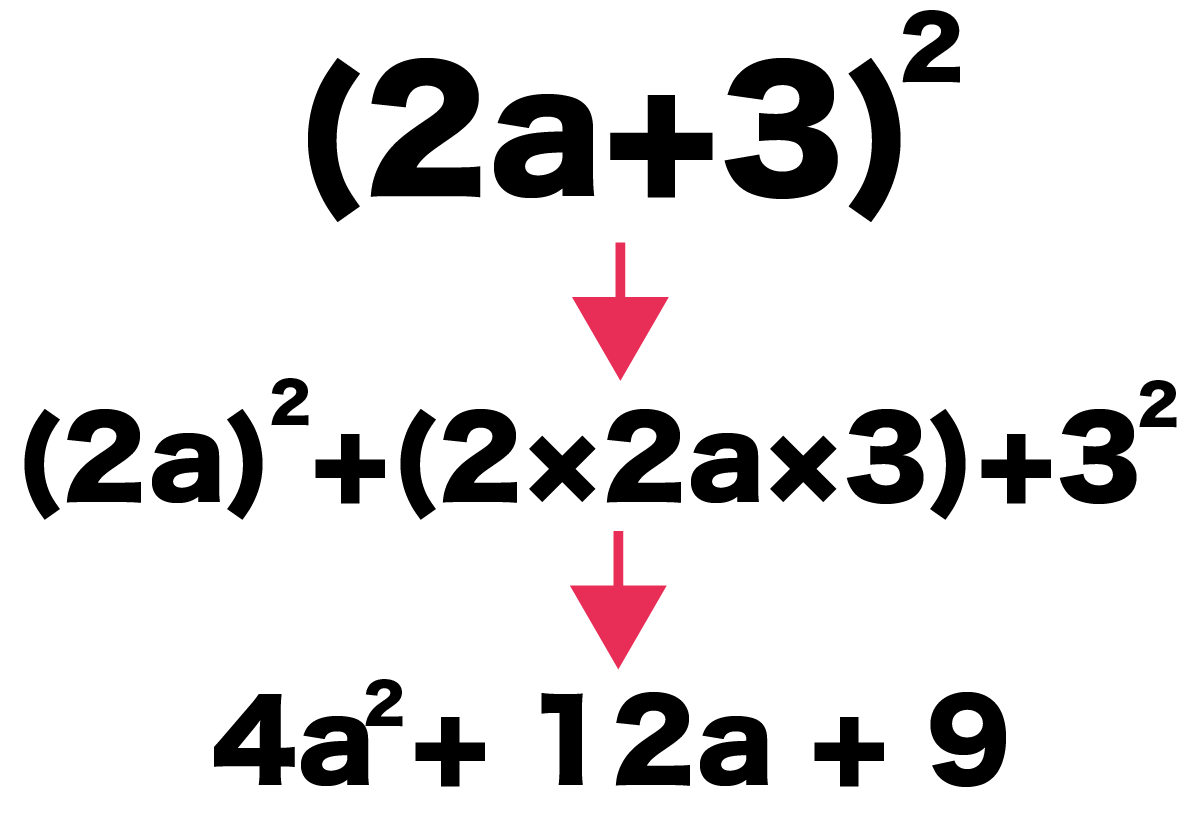
式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく

 回帰分析・最小二乗法の公式の使い方。 公式から分かる回帰直線の性質とは？ 回帰分析とは、 説明変数 x によって目的変数 y の変動を y = f ( x) の形でどの程度説明できるのかを分析 する手法です。 例えば賃貸マンションでは、 部屋が広ければ広いほど三角関数の加法定理，倍角公式，3倍角公式，半角公式 三角関数の和や積には多くの公式がありますが，「加法定理は覚える，他は作る」というのが，作者おすすめの考え方です。・・・ただし，そういう公式があるということと，およその形は記憶にとどめます。 これだけは覚えよう (2)(4)を そもそも乗法公式とは？ 乗法公式とは、名前のとおり「かけ算の公式」で、 （ ）のあるかけ算を展開するのに使われます 。 基本的なものは、中学校で習いましたね。 (x a)(x b) = x2 (a b)x ab ( x a) ( x b) = x 2 ( a b) x a b (a b)2 = a2 2ab b2 ( a b) 2 = a 2 2 a b b 2 (a − b)2 = a2 − 2ab b2 ( a − b) 2 = a 2 − 2 a b b 2

中3の数学は最初が肝心 過去のブログ

いろいろな多項式を展開してみよう 前編 インターネット家庭教師のアスミラ

デジタル大辞泉 乗法公式の用語解説 多項式の積を和の形に直す公式。多項式を展開するときに使う。平方の公式：（a＋b）2＝a2＋2ab＋b2、和と差の積の公式：（ab）（a−b）＝a2−b2、たすきがけの公式：（ax＋b）（cx＋d）＝acx2＋（ad＋bc）x＋bdなど。展開公式。 乗法公式1 乗法公式2 乗法公式3 乗法公式の利用1 乗法公式の利用2 式の証明 式の展開 (利用)平方の公式が適用できます。 今回はこれが適用できます。 という流れになります。 ですので、はじめに見たように、乗法公式で解いてもらってもまったく問題はありません。 ただ、平方の因数分解になっている！って数の感覚を鍛えておくとより速く因数

数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん

中3 数学 乗法公式 まとめ 中学生 数学のノート Clearnote

基本的な乗法公式（展開公式） I (ab)2=a22abb2 II (a−b)2=a2−2abb2 III (ab) (a−b)=a2−b2 ※ これらの公式のうち I～ IVは中学校の復習となっているが，高校の数学 I でもう一度出てくる．公式は中学校と同じでも，扱い方が少し変るところがある

中学数学 式の展開 乗法公式 中学数学の無料オンライン学習サイトchu Su

乗法公式 多項式の展開公式 の覚え方と使い方 数学fun

乗法公式

３次式の乗法公式が成り立つことの証明が分かりません 写真の問3です Clearnote

乗法公式 X A X B Youtube

式と証明 ３次式の展開について 日々是鍛錬 ひびこれたんれん

式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく

多項式の乗法公式を理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに

数 乗法公式とその利用の定期テスト対策問題 解説付 Tekibo

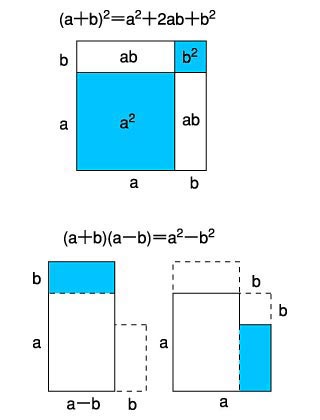
授業実践記録

中3 数学 乗法公式 まとめ 中学生 数学のノート Clearnote

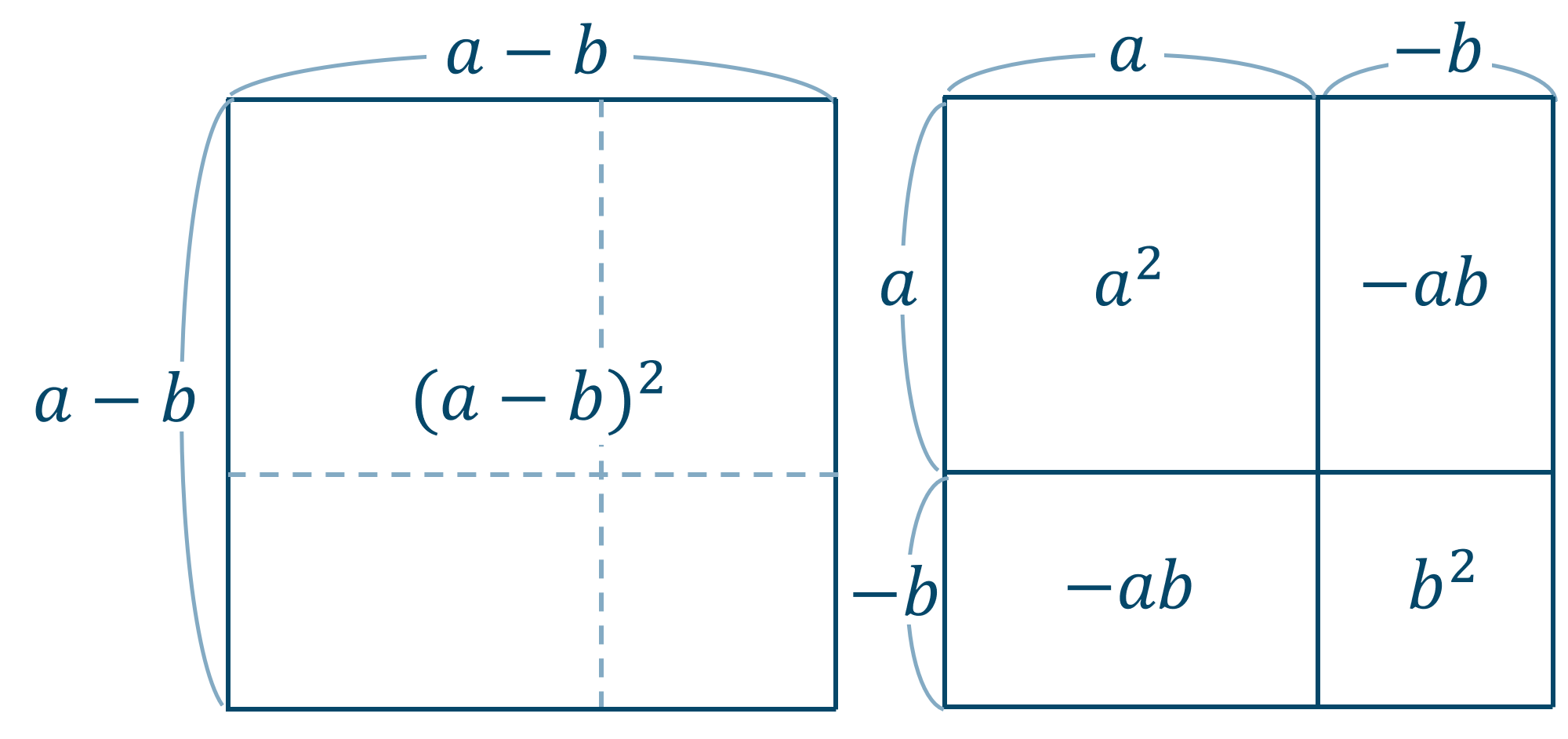
簡単証明 乗法の公式はなぜ使えるんだろう Qikeru 学びを楽しくわかりやすく

式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく

Tossランド 乗法公式による展開 の基礎 基本

乗法公式の利用 いろいろな式の展開 前半 教遊者

モノマナビ研究所

4つの乗法公式 教遊者

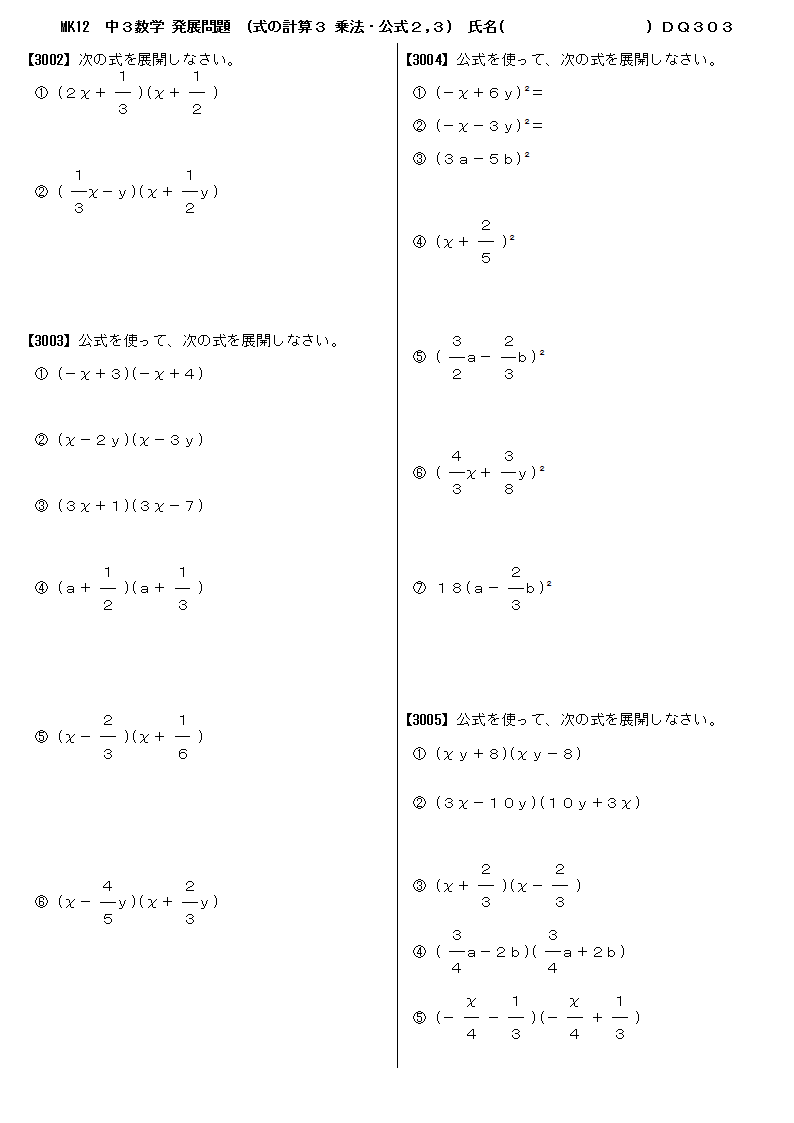
無料 中３数学 発展 応用問題 問題プリント 303 式の計算３ 乗法 公式２ ３

中学３年の数学 乗法の公式について 栄翔塾

乗法公式の視覚的理解 Geogebra

乗法公式による式の展開 効率良い復習 テクニックで勉強 テストが楽しくなるブログ

中３数学 乗法公式 応用 置き換え １ Youtube

乗法公式の覚え方 4つの乗法公式を簡単に覚える方法 数学の面白いこと 役に立つことをまとめたサイト

3分で分かる 多項式とは 加法 減法 乗法についてわかりやすく 合格サプリ

中3 乗法公式 因数分解 平方根 中学生 数学のノート Clearnote

展開の公式 乗法公式 の計算方法を図にしてみました あんず学習塾のメモ 図表置き場

因数分解 効率良い復習 テクニックで勉強 テストが楽しくなるブログ

数ii 三次の乗法公式と因数分解 高校生 数学のノート Clearnote

この分数の乗法公式の解き方がわかりません1分のxにして計算するんでしょうか 丁 Yahoo 知恵袋

3 41第２章平方根の計算 乗法公式と平方根の計算 ユニバーハイスクール 高3

数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん

乗法公式の問題 ａ ｂ ａ ｂ の展開を練習しよう 中学や高校の数学の計算問題

乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係

1

乗法公式 時習館 ゼミナール 高等部

中３数学 式の計算 乗法公式２ 基本問題 ヒント 303 プリント

乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係

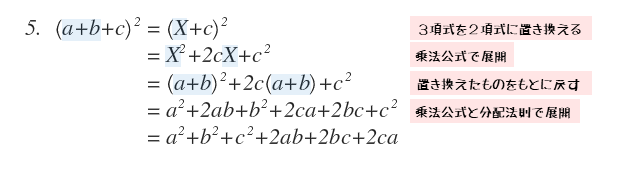
数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん

４月２２日更新 中３一斉授業 数学 展開 乗法公式 担当 中嶋 成績 上がってます 根城学習塾 八戸市

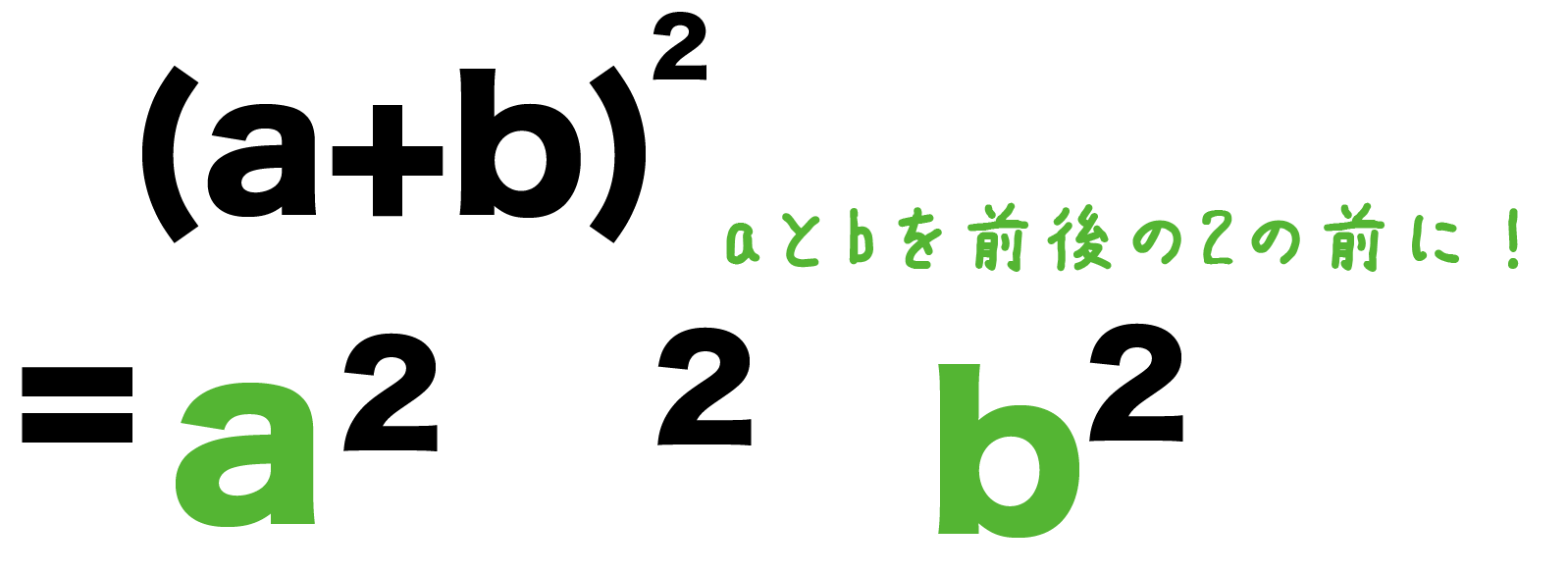
式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく

三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ

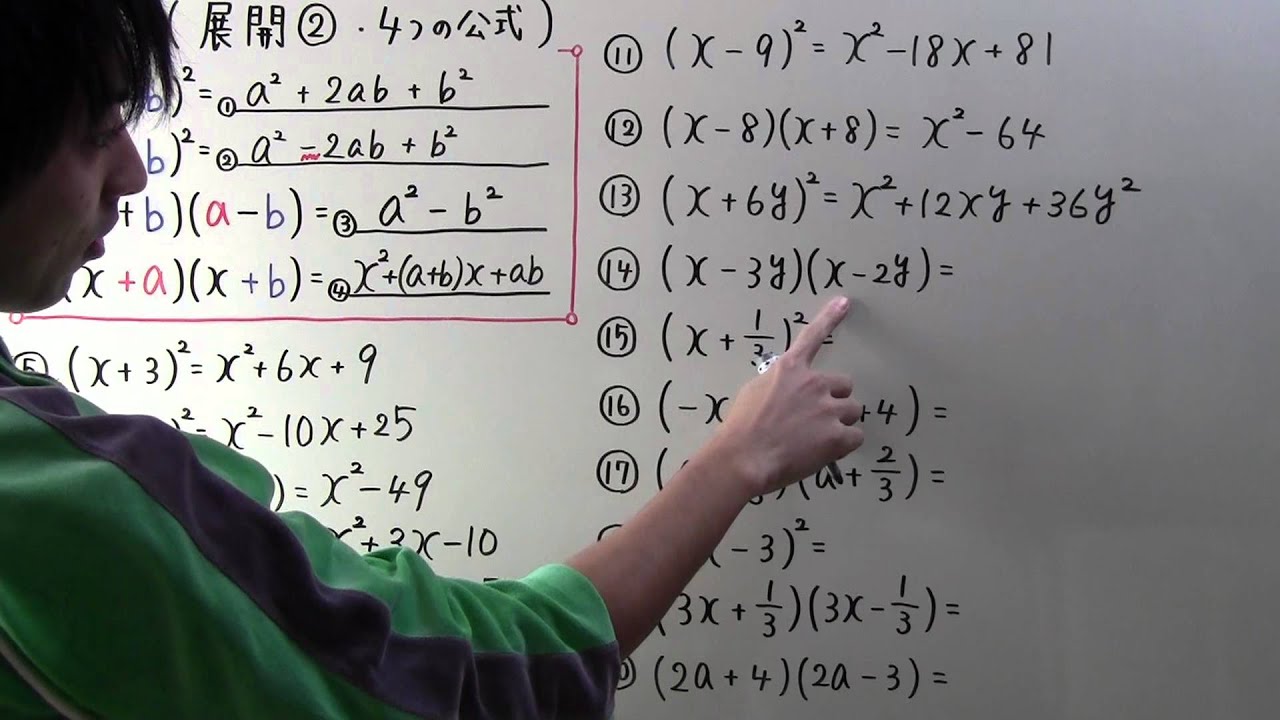
数学 中3 3 展開 4つの公式 Youtube

中3 数学 乗法公式 まとめ 中学生 数学のノート Clearnote

乗法公式を利用した分母の有理化 Youtube

野並英館塾ホームページ 数 3次の乗法公式

中学数学 多項式 の教え方 乗法公式

数学 ２次式の展開のコツと乗法公式 展開公式 ページ 2 教科書より詳しい高校数学

乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学

Tossランド コロナ対応 乗法公式による展開

Studydoctor乗法公式を利用する式の計算 中３数学 Studydoctor

中3 数学 乗法公式 １ 無料学習プリント教材

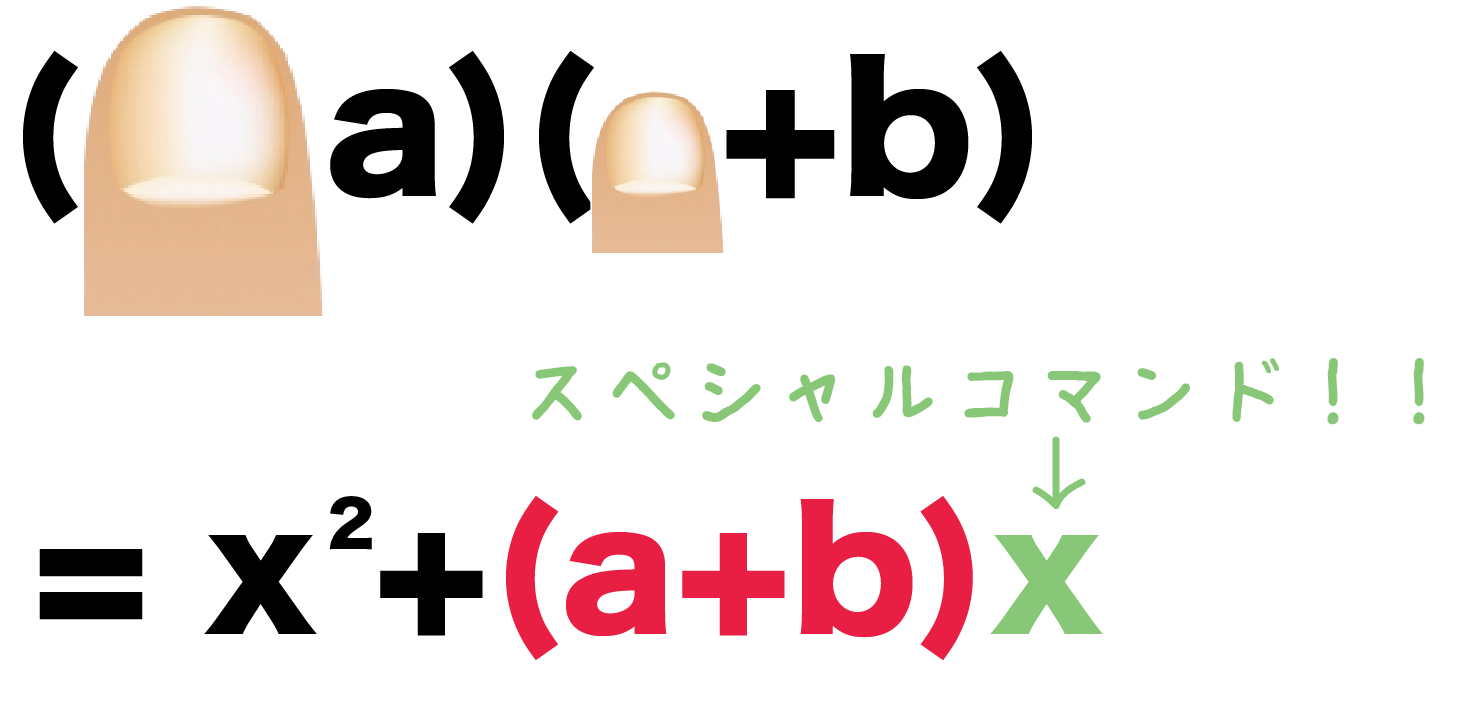
式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく

乗法公式

中学数学3年 展開と乗法公式 受験の月

1

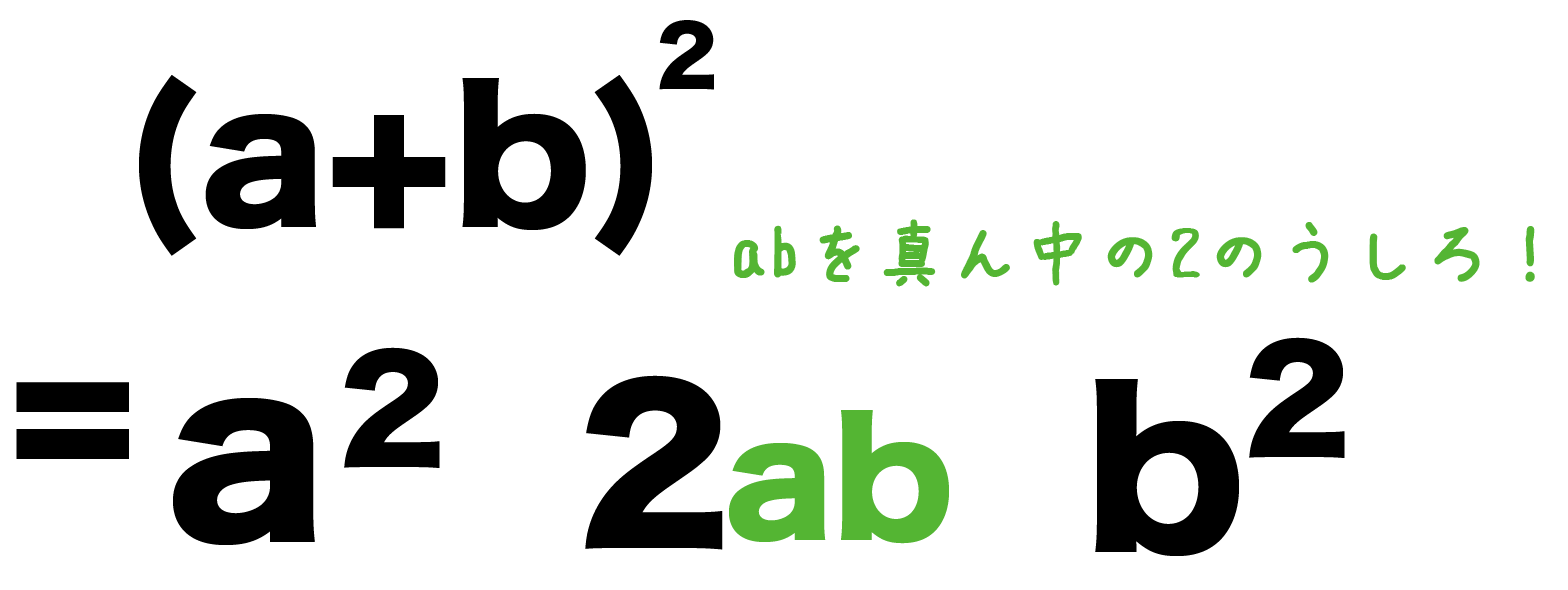
式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく

中3の皆さん 乗法公式マスターしましたか 勉強方法

数学 乗法公式の整理 塾長の備忘録

ม 3 โน ตของ 数学 3年 乗法公式の展開と計算 ช น Clearnote

乗法公式

式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく

数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん

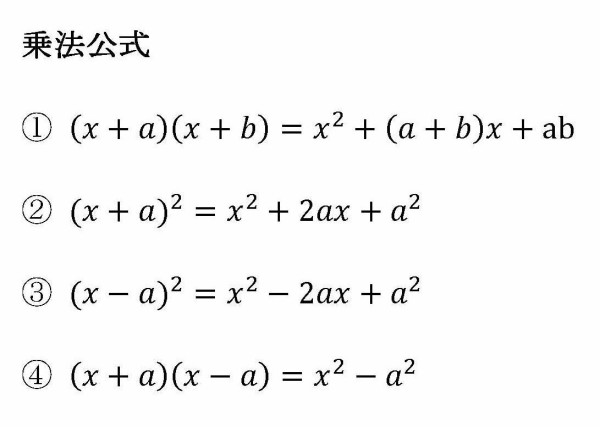
中３数学 乗法公式 桐光学院 竜洋校ブログ

1

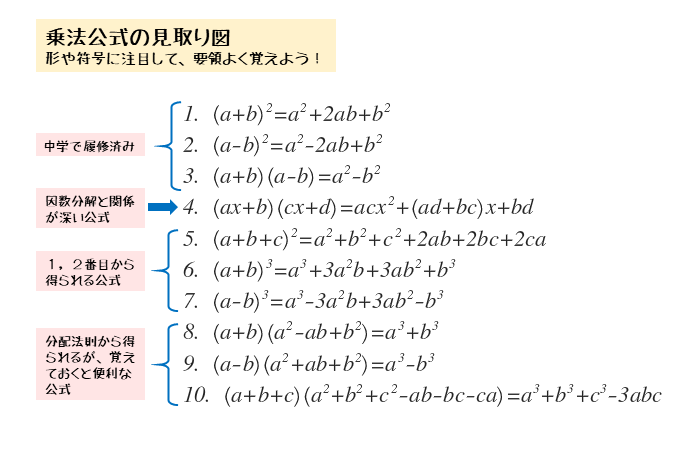
数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん

乗法公式の利用 いろいろな式の展開 前半 教遊者

数探高校講座 数学 数と式 4 乗法公式 数学探究所

乗法公式を利用した計算 Youtube

乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係

無料 中３数学 基本問題 問題プリント 302 式の計算２ 乗法 公式１

4つの乗法公式 教遊者

中学３年数学 乗法公式を利用する式の計算 Youtube

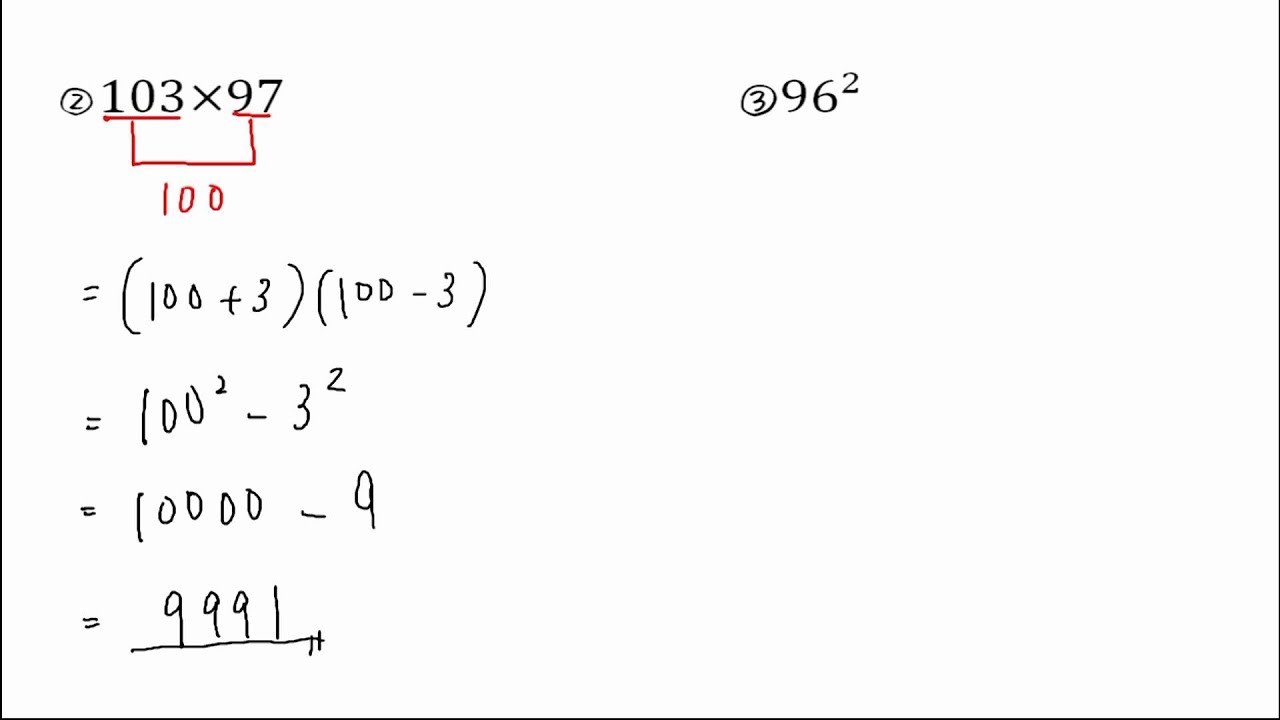
乗法公式を利用した計算 問題 Youtube

ม 3 โน ตของ 数学 3年 乗法公式の展開と計算 ช น Clearnote

乗法公式の利用 いろいろな式の展開 前半 教遊者

3

乗法公式の応用形 名古屋市北区の学習塾は思考力を育む 泰成スクール

中3数学 乗法の公式の定期テスト予想問題 Pikuu

乗法公式

乗法公式

乗法公式の利用 いろいろな式の展開 前半 教遊者

乗法公式まとめ

写真の乗法公式と因数分解の違いってなんですか Clearnote

乗法公式 無料で使える中学学習プリント

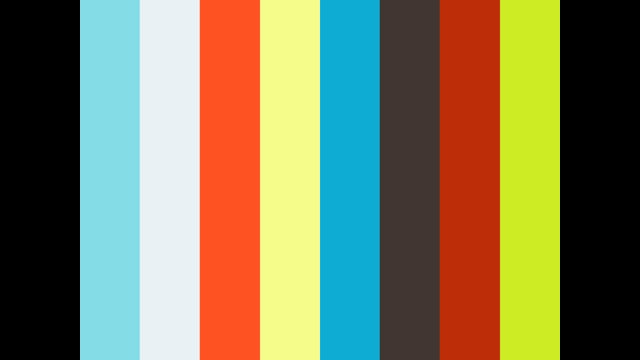
3 5第１章多項式 乗法公式 フロントエンドなブログ

式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく

乗法公式１ ５ 元seの勉強部屋

至急お願い致します 中3 式の計算 乗法公式 式の展開 Clearnote

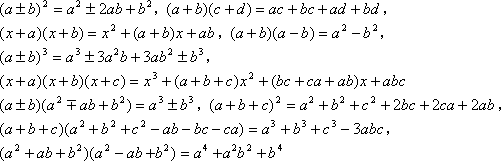
乗法公式 の意味や使い方 Weblio辞書

無料 中３数学 標準問題 問題プリント 302 式の計算２ 乗法 公式１

式と証明 ３次式の展開について 日々是鍛錬 ひびこれたんれん

乗法公式は覚えなくてもいいんじゃないだろうか 学習塾q

乗法公式 因数分解公式 中学生 数学のノート Clearnote

無料 中３数学 基本解説 問題プリント 302 式の計算２ 乗法 公式１